Worked solution to exercise 3.2: Computational complexity of the particle filter

---

Produced in R version 4.4.0.

---

Load packages:

library(tidyverse)
library(pomp)
library(iterators)
library(doFuture)

Construct the pomp object for the Consett measles example

source("model_measSIR.R")

Now run particle filters of several sizes, measuring the amount of time elapses for each one.

expand_grid(
  Np=ceiling(10^seq(1,5,by=0.2))
) -> design

plan(multisession)
foreach (
  expt=iter(design,"row"),
  .combine=bind_rows,
  .options.future=list(seed=TRUE)
) %dofuture% {
  system.time(measSIR |> pfilter(Np=expt$Np))[3] -> expt$time
  expt
} -> resultA

Plot the results and fit a line.

resultA |>
  ggplot(aes(x=Np,y=time))+
  geom_point()+
  geom_smooth(method="lm",formula=y~x)+
  expand_limits(x=0,y=0)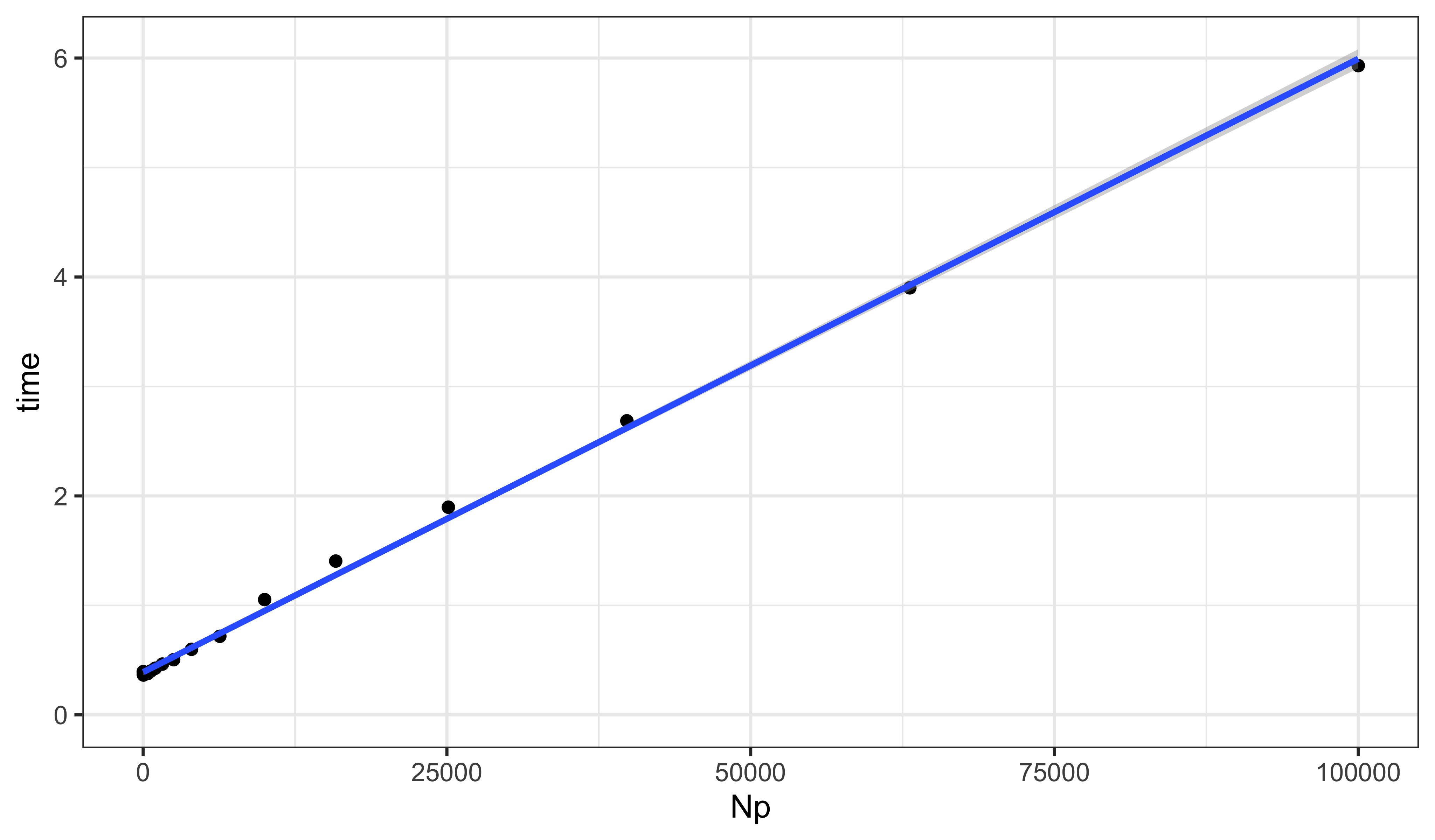

lm(time~Np,data=resultA) -> fit
summary(fit)

Call:
lm(formula = time ~ Np, data = resultA)

Residuals:
      Min        1Q    Median        3Q       Max 
-0.062130 -0.025747 -0.020232 -0.009805  0.126790 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 3.902e-01  1.293e-02   30.19   <2e-16 ***
Np          5.603e-05  4.595e-07  121.93   <2e-16 ***
---
Signif. codes:  
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.05263 on 19 degrees of freedom
Multiple R-squared:  0.9987,    Adjusted R-squared:  0.9987 
F-statistic: 1.487e+04 on 1 and 19 DF,  p-value: < 2.2e-16

The computational expense scales linearly with the number of particles. In this case, we require about 56 μs per 1000 particles.

How does the computation scale with the length of the time series?

measSIR |>
  window(end=21) -> shortMeasSIR

plan(multisession)
foreach (
  expt=iter(design,"row"),
  .combine=bind_rows,
  .options.future=list(seed=TRUE)
) %dofuture% {
  system.time(shortMeasSIR |> pfilter(Np=expt$Np))[3] -> expt$time
  expt
} -> resultB

bind_rows(
  long=resultA,
  short=resultB,
  .id="length"
) |>
  mutate(
    n=case_when(
      length=="short"~length(time(shortMeasSIR)),
      length=="long"~length(time(measSIR))
    )
  ) -> result

result |>
  ggplot(aes(x=Np,y=time,group=n,color=factor(n)))+
  geom_point()+
  labs(color="n")+
  geom_smooth(method="lm",formula=y~x)+
  expand_limits(x=0,y=0)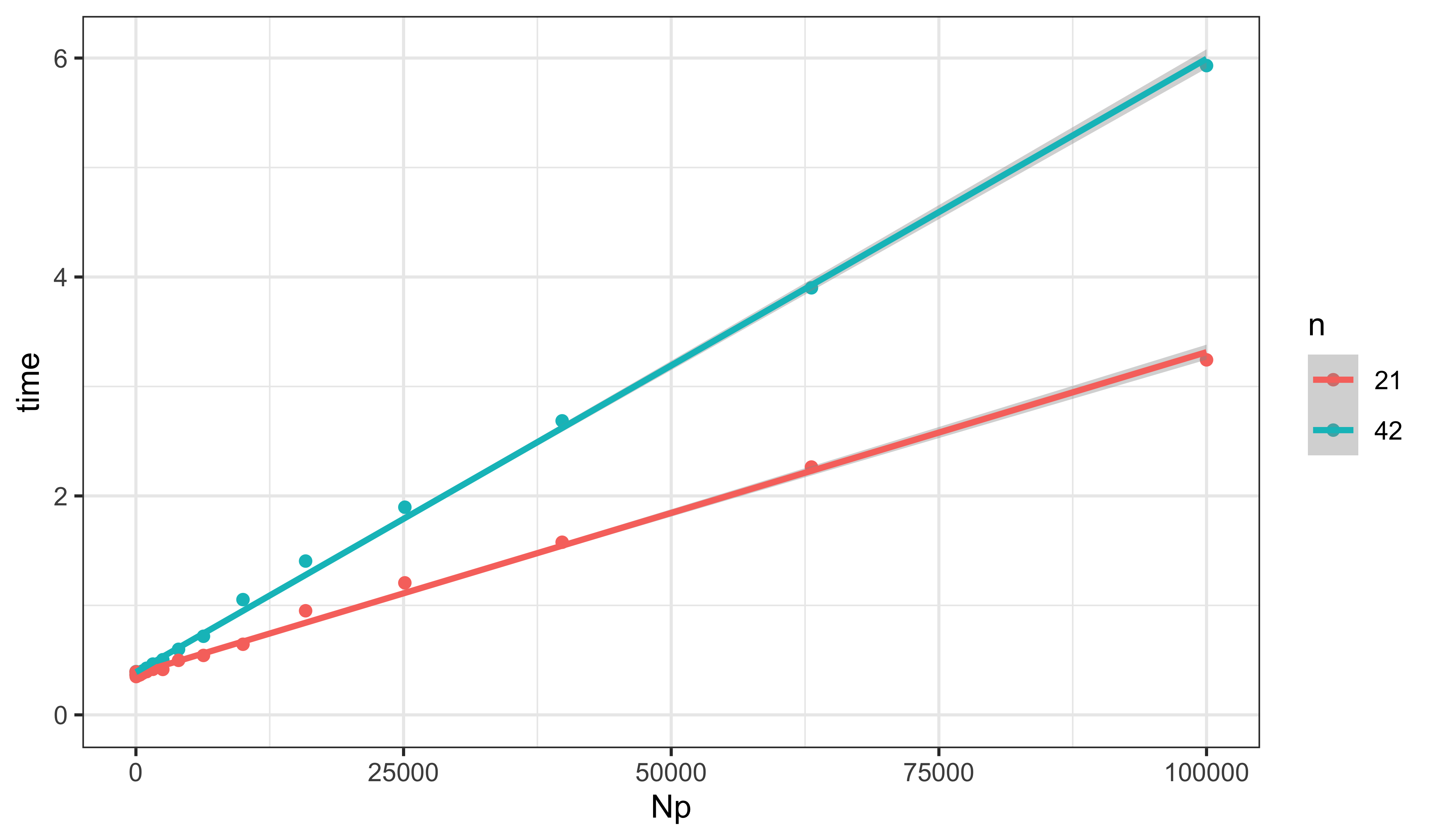

lm(time~n*Np,data=result) -> fit
summary(fit)

Call:
lm(formula = time ~ n * Np, data = result)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.07024 -0.02453 -0.01466  0.00344  0.12679 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 3.618e-01  2.600e-02  13.918  < 2e-16 ***
n           6.757e-04  7.829e-04   0.863  0.39353    
Np          2.715e-06  9.242e-07   2.938  0.00559 ** 
n:Np        1.269e-06  2.784e-08  45.603  < 2e-16 ***
---
Signif. codes:  
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.04734 on 38 degrees of freedom
Multiple R-squared:  0.9984,    Adjusted R-squared:  0.9983 
F-statistic:  8009 on 3 and 38 DF,  p-value: < 2.2e-16

The marginal cost is about 1.3 μs per 1000 particles per data-point.